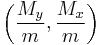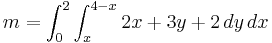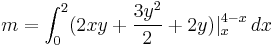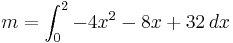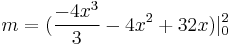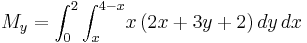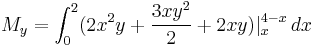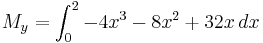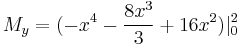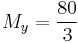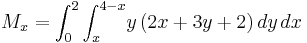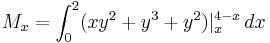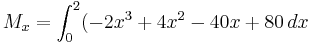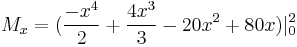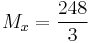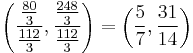Planar lamina

In mathematics, a planar lamina is a closed surface of mass 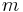m and surface density \rho\ (x,y) such that:

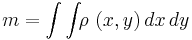m = \int\int_{}{}\rho\ (x,y)\,dx\,dy, over the closed surface.

The center of mass of the lamina is at the point

\left(\frac{M_y}{m},\frac{M_x}{m}\right)

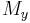where M_y moment of the entire lamin about the x-axis and 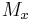M_x moment of the entire lamin about the y-axis.

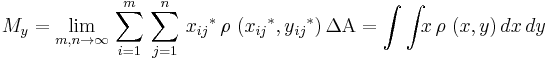M_y = \lim_{m,n \to \infty}\,\sum_{i=1}^{m}\,\sum_{j=1}^{n}\,x{_{ij}}^{*}\,\rho\ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta\Alpha = \int\int_{}{} x\, \rho\ (x,y)\,dx\,dy, over the closed surface.
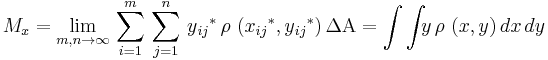M_x = \lim_{m,n \to \infty}\,\sum_{i=1}^{m}\,\sum_{j=1}^{n}\,y{_{ij}}^{*}\,\rho\ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta\Alpha = \int\int_{}{} y\, \rho\ (x,y)\,dx\,dy, over the closed surface.

Example 1.

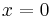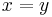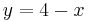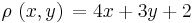Find the center of mass of a lamina with edges given by the lines x=0, x=y and y=4-x, where the density is given as \rho\ (x,y)\,=4x%2B3y%2B2.

m = \int_0^2{\int_x^{4-x}}_{}{}\,2x%2B3y%2B2\,dy\,dx
m=\int_0^2 (2xy%2B\frac{3y^2}{2}%2B2y)|_x^{4-x}\,dx
m=\int_0^2 -4x^2-8x%2B32\,dx
m= (\frac{-4x^3}{3}-4x^2%2B32x)|_0^2
m= \frac{112}{3}
M_y = \int_0^2{\int_x^{4-x}}{}{}x\,(2x%2B3y%2B2)\,dy\,dx
M_y=\int_0^2 (2x^2y%2B\frac{3xy^2}{2}%2B2xy)|_x^{4-x}\,dx
M_y=\int_0^2 -4x^3-8x^2%2B32x\,dx
M_y= (-x^4-\frac{8x^3}{3}%2B16x^2)|_0^2
M_y= \frac{80}{3}
M_x = \int_0^2{\int_x^{4-x}}{}{}y\,(2x%2B3y%2B2)\,dy\,dx
M_x = \int_0^2 (xy^2%2By^3%2By^2)|_x^{4-x}\,dx
M_x = \int_0^2 (-2x^3%2B4x^2-40x%2B80\,dx
M_x= (\frac{-x^4}{2}%2B\frac{4x^3}{3}-20x^2%2B80x)|_0^2
M_x= \frac{248}{3}

center of mass is at the point

\left(\frac{\frac{80}{3}}{\frac{112}{3}},\frac{\frac{248}{3}}{\frac{112}{3}}\right)=\left(\frac{5}{7},\frac{31}{14}\right)

Planar laminas can be used to determine moments of inertia, or center of mass.